Autres cours :
Triangles semblables et isométrie
Équation de droites : systèmes
d'équation.
Équations de droites : systèmes d'équation.
I) Équation de droite
Une égalité traduisant l'appartenance d'un point de coordonés (x ; y) à une droite s'appelle une équation de cette droite.
Propriétés :
- toute droite du plan repéré à une équation
de la forme :
- x = c : si elle est parallèle à l'axe des ordonées.
- y = mx+p (—> équation réduite)
- toute équation de droite peu se mettre sous la forme ax + by + c = 0. Cette équation est dite cartésienne et est verifíé que si x et y ne sont pas simultanément nul.
Preuve :
- si l'équation est de la forme : x = k
alors x-k = 0 avec a=1 b=0 et c=-k. - si l'équation de la droite est de la forme y = mx+p
mx-y+p = 0 est une équation cartésienne ou a=m b=-1 et c=p
Réciproque :
Si l'équation de la droite est de la forme ax+by+c=0
- si b = 0 (et a0) alors ax+c = 0 ou x = -c/a
- si b 0 by = -ac-c ou y = -a/bx - c/b
Théorème :
Dans une base (o, vecteur i, vecteur j, avec vecteur n (x
; y) et vecteur m (x' ; y')
on défini le determinants de ces deux vecteurs
comme det 
= 
= xy'-y'x
dire que vecteurs u et v sont colinéaires, c'est dire que
det = 0
donc = 0
xy'-y'x = 0
Application :
Déterminer une droite qui passe par A (-2;9) et B
(1;-3)
et M (x;y)
(
3;-12) et 
(x+2; y-9)
M est sur (AB) signifie que
et sont
colinéaires
donc det (;
) = 0
3(y-9) - (-12)(x+2) = 0
alors 12x + 3y -3 = 0 est une équation cartésienne de (AB)
II) Caractérisation du parrallélisme.
Définition :
On appelle vecteur directeur d'une droite D, tout vecteur V, non nul de même direction que la droite.
Le vecteur directeur d'une droite indique sa direction. Tout les vecteurs colinéaires au vecteur directeur sont aussi des vecteurs directeurs de la droite.
Définition :
- si une droite à pour équation y = mx + p
alors le vecteur v (1;m) est directeur de cette droite. - si une droite à pour équation ax+by+c=0
alors le vecteur v (-b;a) est directeur de cette droite.
Preuve :
D : y=mx+p
et A et B deux points de cette droite.
A (0;p)
B (1;m+p)
A et B sont deux points de D
donc est
un vecteur directeur de D
alors (1;m)
D : ax+by+c=0
donc y = -a/bx - c/b
alors vecteur v (1; -a/b) est un vecteur directeur de D
soit vecteur u = -b
(on multiplie par -b pour simplifier)
donc (-b;a)
est aussi un vecteur directeur de (AB)
Exemples :
- Soit M(x;y)
M est sur D
donc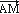
et 
sont
colinéaires.
det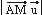
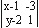= 0
=0
(x-1)1 - (-3)(y-2) = 0
x-1 + 3y-6 = 0
y = -1/3x + 7/3 est une équation réduite de D. - (-3;1)
= -1/3
et
sont des vecteurs directeurs de D.
donc(1;-1/3)
et l'équation reduite de D est de la forme : y = -1/3x+p
or A est sur D, ses coordonées verifient donc l'équation:
2 = -1/3*1+p
p = 7/3
donc l'équation réduite de D est y = -1/3x+7/3
Propriétés :
Deux droites parallèles ont le même coéficient directeur et le même vecteur directeur.
Théorème :
Soit D d'équation ax+by+c=0 et D' d'équation a'x+b'y+c'=0
D et D' sont parrallèls signifie que ab'-a'b = 0
III) Caractérisation de l'orthogonalité.
Théorème :
Soit (x;y)
et (x';y')
et
sont orthogonaux signifie que
xx' + yy' = 0
Remarques :
Soit 
un
repère orthonormé du plan.
Soit D d'équation ax+by+c = 0
(-b;a) est
un vecteur directeur de D
(a;b) est
alors un vecteur normal de D, c'est à dire que
est orthonormal à.
Preuve : (-b;a)
dvient(a;b)
: -ba + ab = 0 doncet
sont orthogonaux.
Exemples :
- Soient D : 3x-5y+7 et D' : 5x+3y+11 = 0
Préciser si D et D' sont perpendiculaire
3*5 + (-5)3 = 15-15 = 0
donc D et D' sont perpendiculaires. - Soit D : 3x-5y+7 = 0.
Déterminer une équation de la droite perpendiculaire à D passant par le point A (-2;1)
D : 3x-5y+7 = 0 donc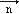(3;-5)
est un vecteur normal de D.
Comme D et D' sont perpendiculaire,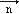
est un vecteur directeur de D'.
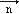(3;-5)
(-b;a) d'où a=-5 et b=-3
D' est donc d'équation : -5x-3y+c = 0
D' passe par A donc ses coordonnées vérifient : -5xa-3ya+c = 0
-5(-2) - 3*1 + c = )
10-3+c = 0
c = 7
alors D' a pour équation -5x + 3y -7 = 0
Système linéaire :
Vocabulaire :
De tels systèmes sont dit linéaires car les équations
quil es composent sont de lignes droites.
On considère le système d'inconue x et y.
Résoudre un tel système c'est déterminer les coules
(x;y) qui vérifient simultanément les 2 équations.
Interprétation graphique :
Il s'agit de deux équations de droites:
résoudre le système reviens à chercher les coordonnées
des points d'intercection de ces deux droites. Trois cas se présentent
;
- si les droites sont séquentes, il y a une seul solution (1 point)
- si les droites sont parrallèles distinctes, il n'y a pas de solution (0 points)
- si les droites sont parrallèles confuse, il y a une infinite de solutions (une infinité de points)
Théorème :
Soit le système :
ax + by + c = 0
a'x + b'y + c' = 0
- si ab' - a'b 0, alors les droites sont séquentes, il y a donc une unique solution.
- si ab' - a'b = 0, alors les droites sont parallèles, il y a soit 0, soit une infinité de solutions.
Application :
5x +y = -7
3x -2y = -12
5(-2)-(3*1) = -10-3 = -13 0
donc il n'y a qu'une seule solution.
y = -7-5x
3x - 2((-7-5x) = -12
y = -7-5x
3x +14 +10x = -12
y = -7-5x
13x = -26
y = -7-5x
x = -2
y = -7 - 5(-2)
x = -2
y =3
x = -2
S = {(3;-2)}.
2002, Jel